この記事では 「サッカーの勝敗予想にディープラーニングを使う」 ということについて経験的に感じたことや、実際に行った記録を残しておきます。専門的な知識については正直ついていけない部分もあります。数式を用いた理論的説明は無理なので、あくまで実践上における 気付き という位置づけでお読みください。
一時は諦めかけていたディープラーニング もしかして使えるかもしれない
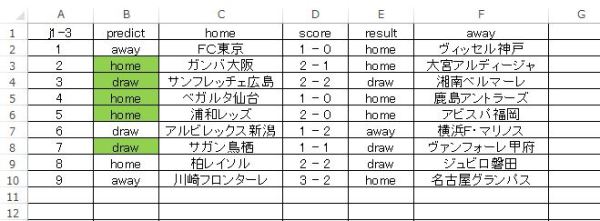
まずは記録を残しておきます。予測対象は J1 第4節 の勝敗についてです。
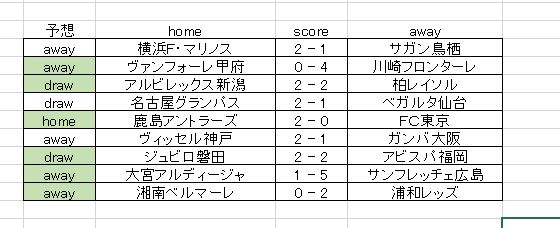 色付き枠が予想が正解している箇所です。これは偶然ではなくて、意味のある出力だと考えています。この予測を吐き出したディープラーニングのセッティングを以下に貼り付けておきます。非常に項目が多いですが、一部を除いて基本的に初期設定のままです。
色付き枠が予想が正解している箇所です。これは偶然ではなくて、意味のある出力だと考えています。この予測を吐き出したディープラーニングのセッティングを以下に貼り付けておきます。非常に項目が多いですが、一部を除いて基本的に初期設定のままです。
label というのが 設定項目のすべてです。level は 設定項目のランクです。critical という表示は実際の H2Oflow には表示されていません。ADVANCE よりも先に表示されている項目が それに当たります。secondary は ADVANCE の項目を指しています。EXPERT はそのままですね。
あと、TYPE というのは 変数の型 のこと。
H2O は JAVA という言語で書かれているのですが、ここで用いる変数には型があるということです。様式に沿って、変数を書く(代入する) ということですね。このあたりはプログラミングの知識がないとまったく理解不能です。調べれば情報はあるので少しづつ理解したいと思います。
actual_value というのが、今回 予測に使用した設定です。
| label | type | level | actual_value | default_value |
| model_id | Key | critical | Grid_DeepLearning_Key_Frame__j1_4_train.hex_model_Mozilla_1459214709783_28_model_7 | |
| training_frame | Key | critical | Key_Frame__j1_4_train.hex | |
| validation_frame | Key | critical | · | |
| nfolds | int | critical | 0 | 0 |
| keep_cross_validation_predictions | boolean | expert | FALSE | FALSE |
| fold_assignment | enum | secondary | AUTO | AUTO |
| fold_column | VecSpecifier | secondary | · | |
| response_column | VecSpecifier | critical | result | |
| ignored_columns | string[] | critical | · | |
| ignore_const_cols | boolean | critical | TRUE | TRUE |
| score_each_iteration | boolean | secondary | FALSE | FALSE |
| weights_column | VecSpecifier | secondary | · | |
| offset_column | VecSpecifier | secondary | · | |
| balance_classes | boolean | secondary | TRUE | FALSE |
| class_sampling_factors | float[] | expert | · | |
| max_after_balance_size | float | expert | 5 | 5 |
| max_confusion_matrix_size | int | secondary | 20 | 20 |
| max_hit_ratio_k | int | secondary | 0 | 0 |
| checkpoint | Key | secondary | · | |
| overwrite_with_best_model | boolean | expert | TRUE | TRUE |
| use_all_factor_levels | boolean | secondary | TRUE | TRUE |
| standardize | boolean | secondary | TRUE | TRUE |
| activation | enum | critical | MaxoutWithDropout | Rectifier |
| hidden | int[] | critical | 200200 | 200200 |
| epochs | double | critical | 10 | 10 |
| train_samples_per_iteration | long | secondary | -2 | -2 |
| target_ratio_comm_to_comp | double | expert | 0.05 | 0.05 |
| seed | long | expert | -4.91277E+18 | 5.33655E+18 |
| adaptive_rate | boolean | secondary | TRUE | TRUE |
| rho | double | expert | 0.99 | 0.99 |
| epsilon | double | expert | 1.00E-08 | 1.00E-08 |
| rate | double | expert | 0.005 | 0.005 |
| rate_annealing | double | expert | 0.000001 | 0.000001 |
| rate_decay | double | expert | 1 | 1 |
| momentum_start | double | expert | 0 | 0 |
| momentum_ramp | double | expert | 1000000 | 1000000 |
| momentum_stable | double | expert | 0 | 0 |
| nesterov_accelerated_gradient | boolean | expert | TRUE | TRUE |
| input_dropout_ratio | double | secondary | 0 | 0 |
| hidden_dropout_ratios | double[] | secondary | · | |
| l1 | double | secondary | 0 | 0 |
| l2 | double | secondary | 0 | 0 |
| max_w2 | float | expert | Infinity | Infinity |
| initial_weight_distribution | enum | expert | Uniform | UniformAdaptive |
| initial_weight_scale | double | expert | 1 | 1 |
| loss | enum | secondary | Automatic | Automatic |
| distribution | enum | secondary | AUTO | AUTO |
| quantile_alpha | double | secondary | 0.5 | 0.5 |
| tweedie_power | double | secondary | 1.5 | 1.5 |
| score_interval | double | secondary | 5 | 5 |
| score_training_samples | long | secondary | 10000 | 10000 |
| score_validation_samples | long | secondary | 0 | 0 |
| score_duty_cycle | double | secondary | 0.1 | 0.1 |
| classification_stop | double | expert | 0 | 0 |
| regression_stop | double | expert | 0.000001 | 0.000001 |
| stopping_rounds | int | secondary | 5 | 5 |
| stopping_metric | enum | secondary | AUTO | AUTO |
| stopping_tolerance | double | secondary | 0 | 0 |
| max_runtime_secs | double | secondary | 28783.618 | 0 |
| score_validation_sampling | enum | expert | Uniform | Uniform |
| diagnostics | boolean | expert | TRUE | TRUE |
| fast_mode | boolean | expert | TRUE | TRUE |
| force_load_balance | boolean | expert | TRUE | TRUE |
| variable_importances | boolean | critical | FALSE | FALSE |
| replicate_training_data | boolean | secondary | TRUE | TRUE |
| single_node_mode | boolean | expert | FALSE | FALSE |
| shuffle_training_data | boolean | expert | FALSE | FALSE |
| missing_values_handling | enum | expert | MeanImputation | MeanImputation |
| quiet_mode | boolean | expert | FALSE | FALSE |
| autoencoder | boolean | secondary | FALSE | FALSE |
| sparse | boolean | expert | FALSE | FALSE |
| col_major | boolean | expert | FALSE | FALSE |
| average_activation | double | expert | 0 | 0 |
| sparsity_beta | double | expert | 0 | 0 |
| max_categorical_features | int | expert | 2147483647 | 2147483647 |
| reproducible | boolean | expert | FALSE | FALSE |
| export_weights_and_biases | boolean | expert | FALSE | FALSE |
| elastic_averaging | boolean | expert | FALSE | FALSE |
| elastic_averaging_moving_rate | double | expert | 0.9 | 0.9 |
| elastic_averaging_regularization | double | expert | 0.001 | 0.001 |
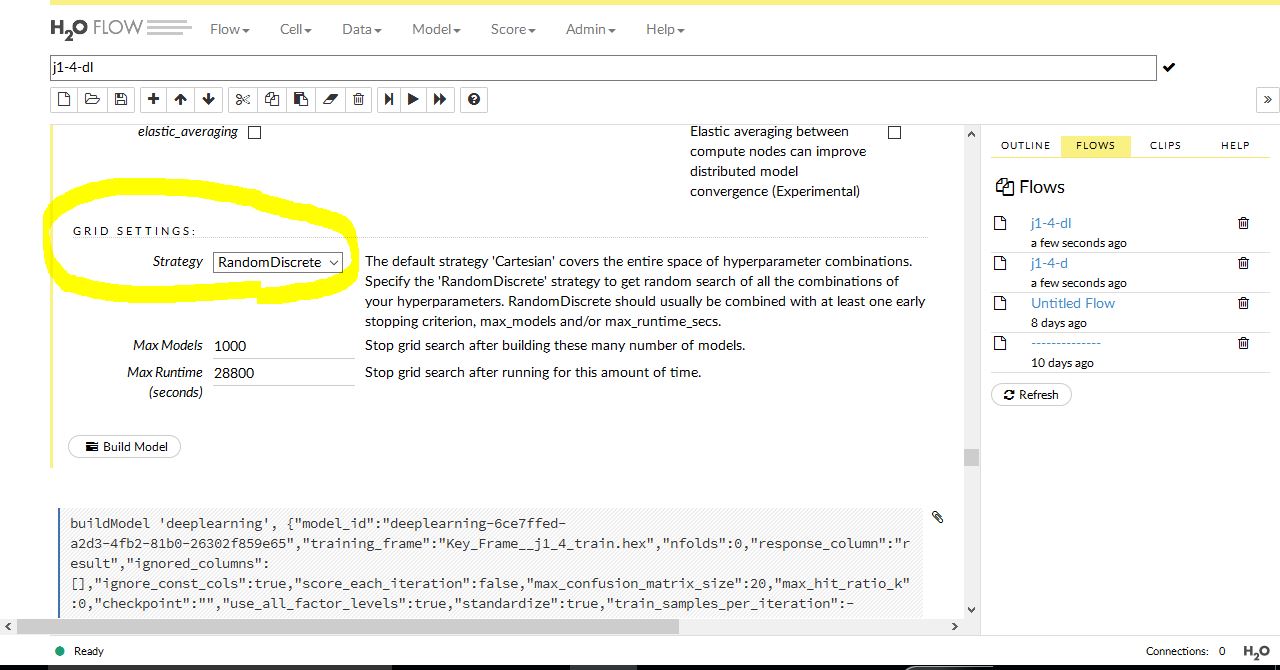
この表には表示されていませんが、グリッドサーチにチェックすると最後に出てくるグリッドセッティングについては以下のようにしてあります。
データ構成やら、このディープラーニングの設定やら いろいろ組み合わせを変えて試してきましたが、やっと意味のある出力が得られたようです。正解率は 6/9 で、それほど高くはありません。しかしランダムフォレストでも同じく 6/9 の正解しか得られていないので悪くない結果だと感じています。
あとは学習に与えるデータ量の問題があります。データを与えれば与えるだけ賢くなるのか? あるいはどこかで制限を加える必要があるのか? 時間が経過しても使えるモデルなのか?
引き続き検証していきます。
ディープラーニングによるトト予想の検証 J1 第3節 でも通用したのか?
J1 第4節 の予測結果をふまえて、第3節でも同様の結果を得ることができたのかどうか? 検証してみました。
H2O に与える データ構成、データ量、そして ディープラーニングの設定にいたるまで すべて同じ様式で予測させてみた結果は以下の通りです。
もちろん データ内容 については、過去の予想時点でしか知り得ない情報のみで予測しています。
色付きが正解で、5枠のみ正解しています。ハズした試合は 4試合 で、個々に試合内容も見てみました。展開によっては あと2枠ほど正解していてもおかしくない内容だとは感じましたが、結果がすべてですので仕方ありませんね。
全体としては やはり意味のある結果を出してくれている印象があります。でたらめに、そして偶然に当てているわけではない感じを受けます。じつはパソコンスペックの問題から、まだ完全にディープラーニングのパラメーターをすべていじっているわけではありません。ご存知かもしれませんが、ディープラーニングはとてもマシンに対する負荷が高いです。今現在 使っている へっぽこパソコンのスペックでは全然パワーが足りません。
予測精度の悪さをマシンのせいにするわけではありませんが、パラメーターのいじり方によっては もっと予測精度が上がる可能性が高いです。環境を整えて再挑戦します。あと J2 のほうも検証してみます。ランダムフォレストではけっこう良い予測ができていましたが、はたしてディープラーニングではどうか? データ構成もよく似ているので同じような結果が出せるんじゃないかと予想しています。
ディープラーニングにおけるサッカー予想においては 毎回 同じ設定では無理がある。その理由を考える。データの示す意味とは
与えられたデータを教師データによってカテゴライズする。それが僕のやっている基本的な内容です。これには 正しく分類されるための前提条件 がふたつあります。
教師データが正しくカテゴライズされていること
同じカテゴリーに属するデータは、同じような特徴量を持っていること(機械が判断できるレベルで という意味)
サッカーの結果は 3way しかありませんので、これを基本に考えると教師データとして間違ったラベルを付けることはまずありません。問題は二つ目にありそうです。これは機械に与えるデータ量とも関係してくると考えています。
問題設定をサッカーにだけ限定して話を進めます。僕の作っている教師データの問題点について ざっくり説明すると以下のようになります。
カテゴリーは同じでも、データの示す内容がまったく異なるケースがいくつもある。
あるいは逆に カテゴリーは違うのに、データ内容が非常に似通っているケースがたくさんある。
こうなると、正しくデータを分類する基準が曖昧になってきて、間違ったラベルを付ける可能性は高くなると考えられます。機械学習で高精度で分類できない原因というのは、ここにあるのではないか?
これらの問題は データをたくさん集めれば集めるほど解消されると考えられがちですが、僕は逆に データ量が大きくなるほど分類精度が落ちるかもしれないと思っています。これはサッカー予想についてだけ考えた場合です。念のため。
もう一つ 念のために書いておきますが、終わった試合について試合内容のスタッツを比較した場合においては、機械学習において ほぼ正しく分類されます。当たり前のことを書いているようですが、スタッツの劣っているチームが勝っていることはまずないです。
あくまで僕が予測のために自作したデータにおいてのみの話です。
以前は ディープラーニング というのは データを与えれば自動的に特徴をつかみ取って、正確に判断してくれる 魔法の箱 のように考えていました。しかし、やはり元になるデータの質というのもかなり重要なのではないかと思います。いくらアルゴリズムが優れていても、デタラメなデータを見せられて、正しく判断、分類しろ といっても無理な話です。
予測モデルについての考え方
ディープラーニングを使った予測モデルの作り方について理解を深めるために、いくつか条件を設定して実際に予測結果を記録してみます。これまでバラバラに トトくじ開催会 ごとに記録してきましたが、継続観察したほうが分かりやすいと思いますので一気に過去にさかのぼって記録します。対象は2016 J1リーグ戦の結果です。1節と2節 についてはデータ作成用に使いますので予想はありません。予測モデルは3節の予想からということになります。
記事の上の方で過去試合について セッティングも貼って結果を表示してありますが、もう一度 設定も変えてテストします。
一般にディープラーニングを使った予測モデルは いったんモデルを作成したら更新しないかぎり古いデータを用いたまま分類なり回帰予測をします。予測モデルを最新の状態にするためには 新しいデータを読み込ませて 再度モデルの構築をしなければなりません。予測モデルの更新についての考え方は事例の性質が全く違いますが リクルートが取り組んでいる事例 などが参考になります。今回は、新しい節の予測に対して 再びモデルを構築する方法をとっています。
上で述べた 予測モデルのアップデートの問題 というのは僕が一番悩んでいる部分でもあります。状況が変化する対象事例において、常に確率的に定量的に測れるデータ構造となっているのかどうか? 特徴量を定量的に測れる事例としては、写真などの画像がありますが、サッカーの試合におけるスタッツなどとは明らかに性質が違います。あと iris などの植物分類とかも性質が違うと思います。株価予想の記事 でも触れていますが、事象によっては 最適なサンプル期間 というのが重要になってくる可能性は高いと思います。それぞれのサンプルに対して もっとも良い予測をするためのパラメーター があるのではないか? サンプル期間 という言葉を トレーニングデータ と置き換えても良い。このように対象とする事象の性質によって、考え方を変える必要があるんじゃないか? そういうように考えて、それぞれの予測モデルでグリッドサーチをしてみて、もっとも適したパラメーターの比較もしてみたいと考えています。
まず最初は J1-3 (今季 J1 第三節 の意)から。
使用するデータは 1節、2節から取ったデータです。これをトレーニングデータとして学習させます。学習のためのディープラーニング各種パラメーターの設定は基本的に初期設定で行います。グリッドサーチしたパラメーターは Activation function だけです。クロスヴァリデーションによるモデル構築は行っていません。
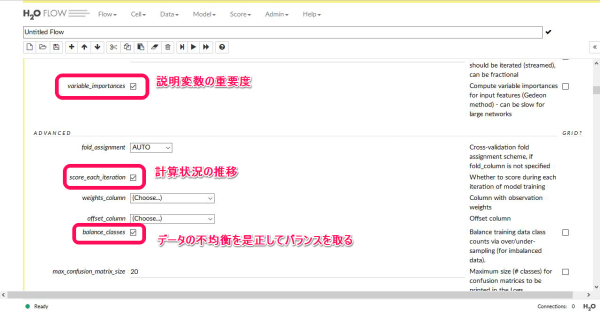
あと、設定画面で左側にある チェックボックス にチェックを入れる項目を示します。これは 最初からグリッドサーチすることなしに この機能をオンにすること を決めている場合にチェックを入れます。具体的には以下のような箇所です。
上のようなチェックボックスには、グリッドサーチが併設されていない項目もあります。初期設定ではいくつかのパラメーターにおいて最初からチェックが入っている項目がありますが、基本的にそれらのチェックは外さない方が良いようです。ドキュメントには初期設定でも それなりにパフォーマンスが得られるように最初からデフォルトでチェックが入れられていることが書かれていました。
僕が最初からチェックを入れた項目は以下の3か所です。
- variable_importances
- score_each_iteration
- balance_classes
デフォルトでチェックが入っている項目はいじりません。最後の Grid Settings は、’Cartesian’ のままビルドを行いました。もうひとつ重要な設定があります。それは input_dropout_ratio という項目です。
H2O においては 0.1 もしくは 0.2 が推薦されていますので、今回は 0.1 をすべてのモデル構築で記入しました。今のところ L1,L2 といった正則化については ゼロ のままモデルにしています。本当は大事なところのようではありますが、知識が追い付いていません。
H2O は java で書かれていて、型によって具体的な数値の代入をするわけですが、このあたりがよく分からないです。つまりはメソッドにしたがって数値をいくつか記入するか、あるいは数値の範囲を示して、それをグリッドサーチして適正な値を得ればよい という理解でいいのか?
モデル構築において活性化関数が仮に ドロップアウト付き(with~) に選択された場合、デフォルトでは 0.5 50% という数値が採用されます。
前置きが長くなりましたが肝心なところのみを書きます。グリッドサーチを使ってモデル構築をすると、いくつかモデルが作成され、それがずらっと示されます。どのモデルが一番良いか? それを決めているのは評価関数の数値です。一般にモデル評価は log loss の値で示されます。数値がゼロに近いほど良いモデルになります。H2O においても log loss で示されます。モデルの並び順は この数値が低いものから順に並んでいます。したがって選択すべきモデルは、一番トップに表示されているモデルということになります。
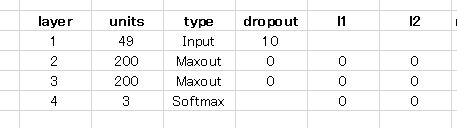
J1-3 で示されたモデルにおいて選択された活性化関数は Maxout でした。層の構造は以下のようになっています。
| layer | units | type | dropout | l1 | l2 |
| 1 | 48 | Input | 10 | ||
| 2 | 200 | Maxout | 0 | 0 | 0 |
| 3 | 200 | Maxout | 0 | 0 | 0 |
| 4 | 3 | Softmax | 0 | 0 |
この表には続きがあって、統計的数値 たとえば 平均的重み とか、二乗平均平方根、バイアスの傾向など数値が続きます。正直言って 評価の方法すら分かりません。
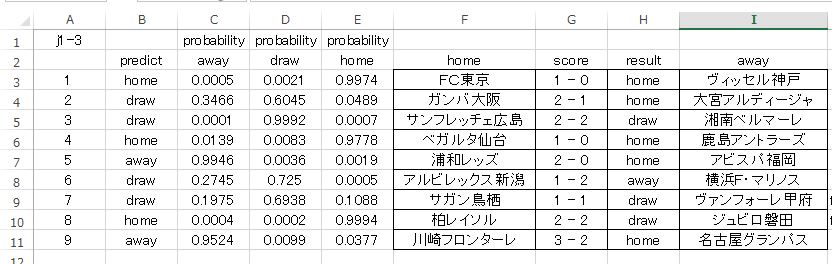
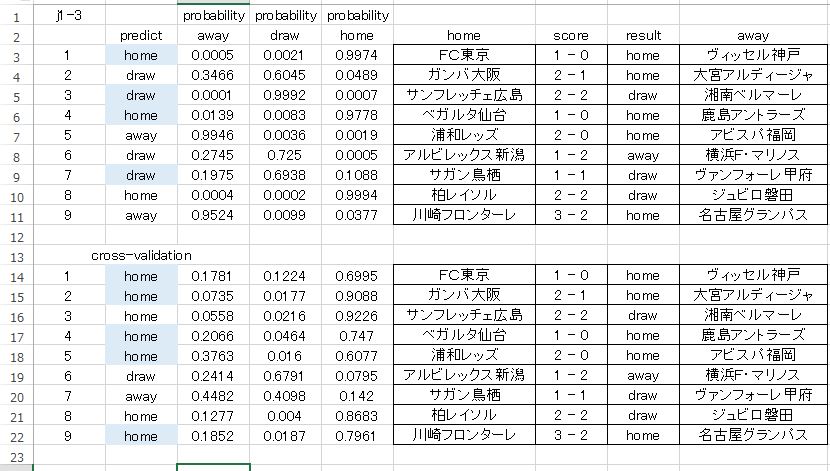
次に、このモデルを使った実際の予測を載せます。実務上はこれから挙げる結果が何よりも重要です。難しい数値で理解するよりも、どれだけ正しい予測ができたか? というのが評価の方法としては一番分かりやすいし重要なことです。
確率の順序が away,draw,home となっていますので注意してください。ストレートで当たっているのが 4枠 です。あまり良くはありません。第二候補まで見ても(ダブル購入を前提とする)6枠までしかフォローしていませんね。
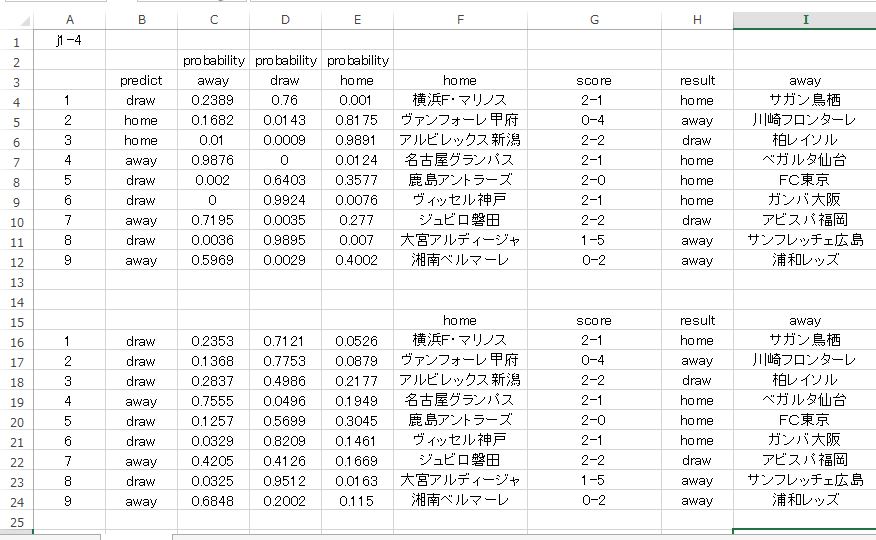
続いて J1-4 です。層構造、実際の予測を挙げます。
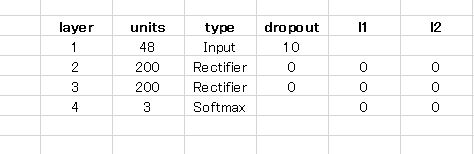 TYPE のところ 活性化関数 に Rectifier が選択されています。これは僕が選択したわけではなくて、グリッドサーチ で選択されました。
TYPE のところ 活性化関数 に Rectifier が選択されています。これは僕が選択したわけではなくて、グリッドサーチ で選択されました。
 予測結果はものすごく悪いです。モデル構築の際には 交差検定 をしていません。つまり このモデルはトレーニングデータのみに当てはまるものであって、汎化性能 が低いモデルだということです。j1-3 と同じセッティングだったのにずいぶん違いがあります。関数ひとつでものすごく結果が違います。使用したデータは累積タイプのものです。つまり 1節分 だけ先の予測よりインスタンスが増えています。
予測結果はものすごく悪いです。モデル構築の際には 交差検定 をしていません。つまり このモデルはトレーニングデータのみに当てはまるものであって、汎化性能 が低いモデルだということです。j1-3 と同じセッティングだったのにずいぶん違いがあります。関数ひとつでものすごく結果が違います。使用したデータは累積タイプのものです。つまり 1節分 だけ先の予測よりインスタンスが増えています。
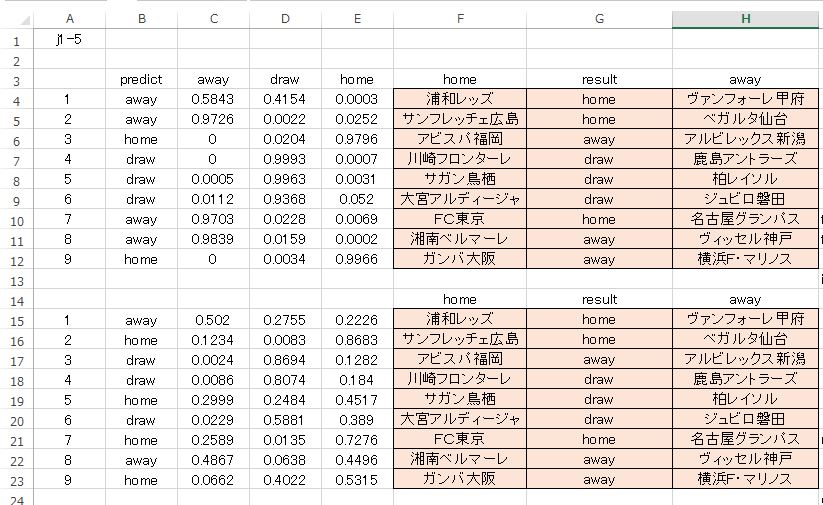
三つ目の J1-5 です。
トレーニング用データは上と同じく 累積です。活性化関数もグリッドサーチをかけています。その他の設定も全く同じで、グリッドサーチをかけるところはすべて同じ、またチェックボックスへのマークもすべて同じです。
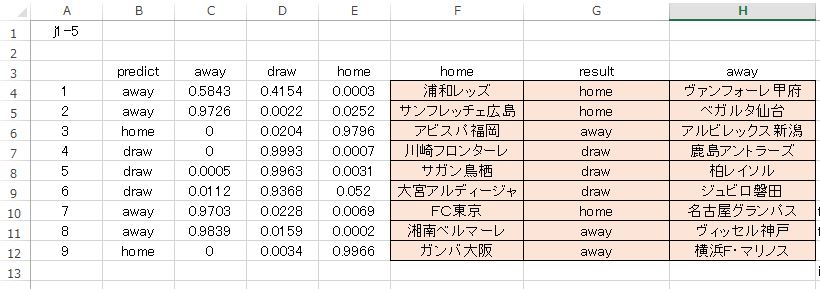 真ん中の 4,5,6枠 の DRAW の正解が目を引きますけど、全体としては トンチンカン ですね。使えません。
真ん中の 4,5,6枠 の DRAW の正解が目を引きますけど、全体としては トンチンカン ですね。使えません。
結局のところ 何が言いたいか というと、最適なパラメーターセッティング というのは データに大きく依存するということ。トレーニングデータに大きく左右されます。グリッドサーチはあくまで与えられたトレーニングデータに対してのみ最適な値を返そうとするだけで、それが必ずしも目的に適った値ではないということです。
次はクロスバリデーションを使って、どのように変化するか? 同じように検証してみます。
H2O クロスバリデーション を使った予測について
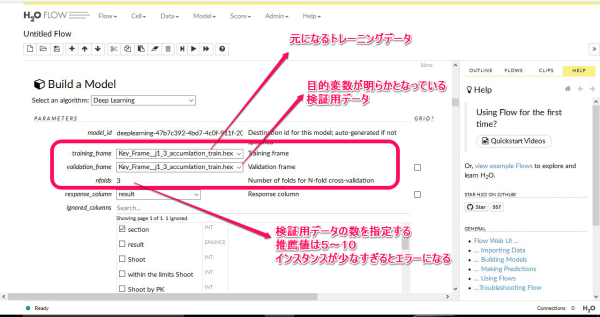
j1-3 (J1 第3節)の予測です。モデルタイプを選択すると、以下のようなボックスが表示されます。画像について少し補足説明をします。
まず トレーニングフレーム には、元になる教師データを選択します。これはすでにアップロードしてパースしてあるものが一覧表示されます。そこから選択するだけです。
その下のフレームには、すでに目的変数が分かっている(入力してある状態)のデータを選択します。これもあらかじめアップロード、パースしておくと選択画面に一覧表示されます。データフレームの型は完全に一致している必要があります。
画像の例では、教師データと検証用データが同じになっています。この意味は、元データを いくつかのデータに分割して、(インスタンスの内容は入れ替えがしてある)そのそれぞれのデータに対してモデル構築をする という意味です。そして検証用データにもっともフィットする予測モデルを構築してくれます。
つまり、特定の教師データのみにフィットするモデルではなくて、ある程度 汎化性能を持たせるために、こういうことをやらせるわけです。たぶん。検証データ はべつに元データである必要はなくて、自分であらかじめ検証用としてデータをいくつか用意して、それらをまとめて指定することもできます。その場合は右側のチェックボックスをオンにします。すると選択可能なデータが一覧表示されるので、あとは選ぶだけです。
N-fold というのは いくつのデータを検証用として作成するか? というもので、H2O の推薦値としては 5~10 となっています。画像では 3 になっていますが、これは インスタンス の数が少なすぎるからです。やむを得ず 3 にしたまでですので真似しないでください。
J1-3 のクロスバリデーションによる予測モデルは以下のようになりました。セッティングは上の記事にある J1-3 とまったく同じです。
| layer | units | type | dropout | l1 | l2 | mean_rate | rate_RMS | momentum | mean_weight | weight_RMS | mean_bias | bias_RMS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 48 | Input | 10.0 | ||||||||||
| 2 | 200 | TanhDropout | 50.0 | 0 | 0 | 0.0060 | 0.0061 | 0 | 0.0003 | 0.0928 | -0.0002 | 0.0021 | |
| 3 | 200 | TanhDropout | 50.0 | 0 | 0 | 0.0155 | 0.0193 | 0 | -0.0001 | 0.0696 | 0.0003 | 0.0052 | |
| 4 | 3 | Softmax | 0 | 0 | 0.0100 | 0.0069 | 0 | 0.0116 | 0.3922 | -0.0051 | 0.0099 |
活性化関数にドロップアウトが付いてきました。実際の予測結果の比較は以下。
色付きは正解枠です。微妙な結果ですが 1枠 正解が増えています。
j1-4 のクロスバリデーション予測結果です。活性化関数は TanhWithDropout となっています。
ストレートで当たっているのは2枠のみという寂しい結果となっています。自分なりの見方では 確率 に注目しています。微妙な結果ですが それなりに意味のある結果が出力されていると感じます。
ちなみに クロスバリデーションを行うと 設定項目のエキスパートに keep_cross_validation_predictions というチェックボックスが表示されますが、ここはオフにしてあります。
最後に j1-5 のクロスバリデーションを用いた予測結果を示します。活性化関数はRectifierWithDropout が選択されています。
ストレートでの当たりは 5枠 です。正解が1枠増えましたが まだまだダメです。使えません。今回のクロスバリデーション、検証用に指定した数 j1-3 以外はすべて 5 でした。全体的な印象としては 少し正解率がアップしたかな という感じです。データ量が増えれば、選択される活性化関数も安定してくるのかもしれません。今は 与えるデータセットによって バラバラ です。これから考えられることは、データの持つ 質 というか 性質 が、それぞれに特徴が違う という可能性が考えられます。シーズンを通して検証する価値はあるかもしれません。
もう一つの気付きとしては、グリッドサーチで選択される 活性化関数 についてです。交差検定をしない方では、ドロップアウトが選択されることはありませんでしたが、クロスバリデーションを用いた予測モデルではすべてにドロップアウトが付いたこと。これはなぜか?
専門的知識がないので何とも言えませんけど、おそらく汎化性能を高めるために、中間層において情報の伝達量を半分に制限したのだろうと思います。間違った理解をしているのかもしれませんが。
現段階では、実際に予想を組み立てる場合の使い道としては、ダブルで考えるならどれを選ぶか? という場面で使えるかもしれません。つまり本命以外に あとひとつ選ぶならどれ? という感じで。しかしながら、まったくの的外れの枠もあるのでもう少し精度を上げたいところです。
また気づきがありましたら追記するかもしれません。おわり。


コメント