第８９４回　トトくじ予想　

第８９４回　トトくじ予想　機械学習による予想だけどいつもと違うやり方

今回のトトくじ予想に使ったのは標準偏差です。詳しい考え方は追記する予定。まずは予測表です。以下は変動係数による予測です。

かなり変かも。　大スベリかなぁ？

予想の考え方

キーワードは三つあります。平均値、標準偏差、変動係数　です。以下に予想に用いた表を載せます。

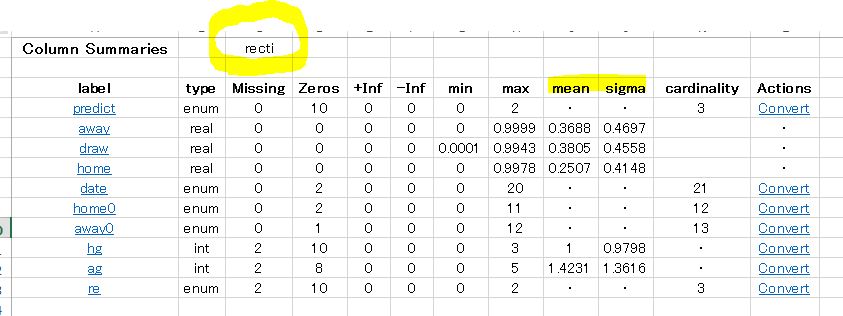上の画像は　１枠目　ハンブルガーＳＶ　ー　ＦＣアウグスブルク　のもので、予測モデルを表しています。。予測スキームは　H2O　ディープラーニング　rectifier 　です。　実際の予測結果は　VIEW　で確認することができます。注目するところは黄色マーキングした　MEAN　と、SIGMA　です。平均と標準偏差ですね。

mean　の意味するところは、この予測モデルにおける分類確率の平均値を表しています。sigma　は、分類確率の平均値に対するそれぞれの偏差の平均です。

モデル化された平均分類確率の　「ばらつき加減」　を数値化したものが　sigma　です。

変動係数はこの表には示されていません。計算のしかたは、シグマを平均で割ります。こうするとそれぞれの変動率を比較することができます。実際に計算すると、変動率が異様に高いです。これはそもそもデータに問題があるか、もしくは手法が適切ではない可能性が高いのですが、あえて使っています。

一応、評価の方法としては、一番数値が低いものを選びます。よりバラつきの少ない方を信頼するわけです。検証の結果では完璧ではありませんけど、それなりに信頼できるのかなぁ　という感じ。VIEWで確認できる実際の予測結果とは必ずしも一致するわけではないことに注意してください。

 ナゾの計算による予測

じつはもうひとつ　計算手法　を考案したのですが、理論的に考えて　「これ　どうなの？」　というものがあります。詳しくは書きませんが、考え方としては、これも　「バラツキの小さいもの」　を「より信頼できる」　として選択します。

要するに、予測モデルにおける分類確率というものに対して、どうやって信頼性を測るか？　ということです。単純に確率の大きいものを選ぶのではなくて、「その数値の信頼性」　に重きを置いた予想というわけです。

こちらもかなり変な予想です。自信あるか？　と言われれば　「あんまりないっす・・」　大きくすべるか、そこそこ当たるかのどっちかじゃないかなぁ。

 最終予想　コレでいくわ

さて、締め切りも迫ってきました。ここで最終予想を出します。

２枠目、９枠目　のふたつ・・・支持率はかなり偏ってますが、どうなるでしょうか？　注目ですね。

結果を見る　大ハズレとなった今回の予想について

さて、予想はひどいハズレっぷりです。びっくりしましたね。まさか・・・という感じです。同じ手法が全く通用しないというのは、以前からよくあることなのですが、やっぱり気落ちします。

どうしてこうなった？　っていうのをやはり考えていかなければ前に進めません。詳しい検証は別ページでやるつもりです。

こりゃあかん・・検証のためのアイデアがまったく出ない。

さて、今回の予想について考えるために、いろいろ数字を見直して考えていたのですが・・・まったく見当がつかないという事態に。

そもそも　sigma 　という数値。　コレの意味を自分自身が正確に把握していない可能性があります。統計においてシグマといえば、総和、あるいは　標準偏差　を表すものだと思います。しかし、σ　（シグマ）　だとすれば、異様に数値が大きいし、そしてバラつきも大きすぎる。

「そういうデータなんだ」　ということで納得するしかないのかなとも思いますし、機械そのもの（H2O）に欠陥があるわけでもないです。

と考えた方が自然かなぁという結論に。

全体として、上手く説明できる部分もあれば、まったくトンチンカンな部分もあるという、歯切れの悪い結果となりました。ちょっと見直しのための時間が欲しい。