第892回 海外トトくじ予想はこれだ
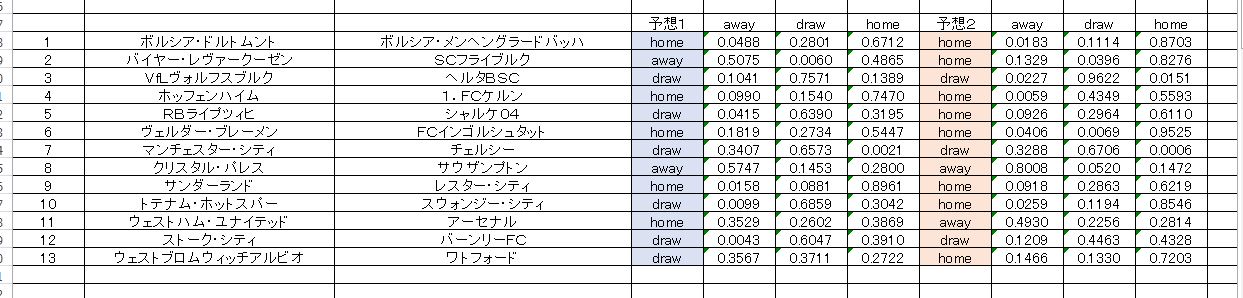
予想の考え方については終わってから追記しようかと。まずは分類確率を示しておきます。
はい、いつもながら画像が小さいのでパソコンなどで別枠で開いて確認お願いします。色付き枠は2種類の予想における第一候補です。
ブルーは単一のアルゴリズムによる予想。ピンクは若干細工がしてあり、ほんの少しですが枠ごとに手を加えてあります。私の予想、期待されてる方はほとんどいないと思われますが、仮に参考になされるなら、分類確率にも注意を払っていただけると良いかと思います。
自分自身についてはマルチの組み立てについて、まだ良いアイデアがあるわけではないです。この表から適当に数値を読み取って組み合わせようかと思っています。なかなか確信が持てる予想というのはできそうでできないものですね。あっさりとハズレになるかもしれないのに、何万円もサクッとつぎ込めるワケがない。
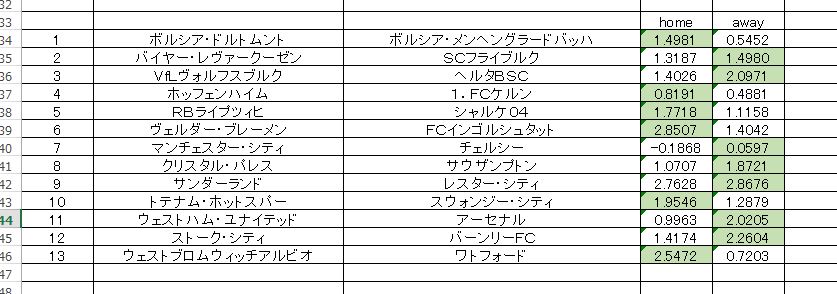
ゴール指数による予測
追加の参考予想として、ゴール数に注目したものをひとつ挙げておきます。指数と言っていますけど、実際のゴール数として考えてもらえばいい。テストの結果からみると、表示されている数値は実際のゴールの数とはそれほど離れることはないです。これは予測された数値に関してではなくて、あくまで過去事例の検証においてのことです。実際にはかなりズレることも考えられますので注意が必要。
ゴール数を数値として回帰予測しただけのものですが、小数点以下の数値の丸め方に関しては、四捨五入のような明確なルールがあるわけではありません。たとえば、 ”1.2” であっても ”2” であるとか、逆に ”1.6” が、 ”1” だとか そういうふうに解釈されることもあります。このあたりの判断は機械にやらせようと考えたのですが、どうも上手く機能しないですね。やってやれないことはないです。しかし結果を見るとドロー判定が多くて、どうも上手く計算されていない気がします。
というわけで、これらの数値は対戦組み合わせにおける ”ゴール状況” を予測したものと考えたほうが良いかもしれないです。(実際のゴール数予測ではなくて)
薄いグリーンマークの方が ”優勢” という意味です。マイナスは ゼロ とみてください。このやり方ですと、少数の扱いが難しいですね。繰り上げ、切り捨て で、どっちにでも解釈できる。全部の可能性を考えると組み合わせが多くなりすぎてしまいます。
確率分布という考え方
過去データを使って未来予測を行うことを考えた場合に避けることができないものに 確率分布 があると思います。私が行っている トト予想 も例外ではなく、おおよそ過去事例から見て、「たぶんここだろう」 という予測地点を割り出しているはず。
ここから導かれることは、要するに 頻度 であり、「事例が多いものは、今後も多く起こり得る」 という推論のもとに すべての予測が行われる。ここであらためて サッカー勝敗 について考えてみると、果たして過去事例の頻度というものが、本当に予測に対して有効なのかどうか? 検証してみる必要があると思います。
いや、検証する必要もないかもしれないですね。それは予想を裏切られる経験をした人すべてが感じていることだから。
私自身の答えは NO です。過去事例のみによる推論ではどうしても無理があると考えます。仮に YES ならば、それは順当結果しか予測できないし、波乱 などというものは決して導かれません。
正確に言うなら次のようになるでしょうか。
過去事例による推論によってある程度は分布にしたがって予測できる。しかし、分布だけでは説明できない事例も数多くある。「どうしてそうなったか」 というような説明ができない事例は、全体から見ると少数かもしれないが、それを 偶然による偏り と片付けてしまっては本質的な部分を見逃してしまう可能性がある。どこかに必ず要因があるはずで、確率分布による推論だけでは不十分である。
非常に堅苦しい言い方だけど、過去事例による分布に従わないものが 波乱 である というわけ。矛盾したことだけど、過去事例に従った分布しか分からない状況において、過去事例から外れた予測をする 、あるいは しなければならないわけですね。
んで、これを実現するために、どういった方法を考えなければならないのか?
あるいは 数式 で書ける人なら、どんな風に書くか? 人力予想 で考えるならどんな風にでも考えることはできます。僕が望むのは、理論的に書くなら どう描くか? ということ。そして、それをアルゴリズムとして表現すること。
いただいたコメントが分布に関することだったので、ちょっと考えちゃいましたね。
「考えを数式で表現する」 ということに関しては、かなり興味があります。同時に勉強も必要であることは痛感しているんですけどね。
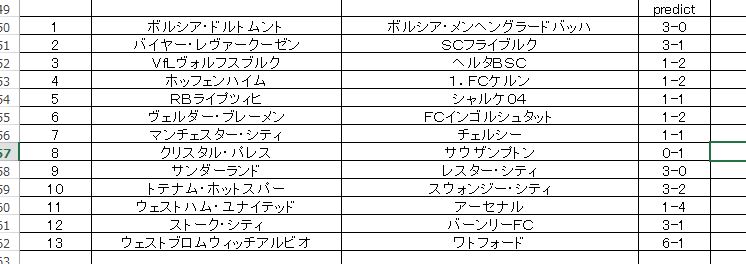
スコアによる分類予測
891回 トトくじは、もう締め切られて買うことはできませんが、予想ネタ としてスコアそのものによる分類予測を挙げておきましょう。
予測結果は以下のようになりました。
これは各チームについてスコアそのものを 予測対象 として分類したもの。 各枠について詳細な分類確率も出しています。PREDICT として表示されているのはその中で一番確率の高いものです。信頼性がどれくらいのものかは検証不足であり、まったくの見当違いといった枠もあるかと思います。
おそらくいくつかは スコアとしては誤答でも 勝敗 といった部分で正解しているだろうと思います。13枠全体としては 中途半端に正解と誤りが混在した形になるだろうと予想します。
ちなみに上記の予想においては 1-2-3番人気 が、8-2-3 となり、100万円ぐらいの配当が期待されています。 ほぼ順当寄り の予想というわけですね。あんまり面白い予想ではありません。 マークの振り分けについてもほぼ平均といったところで、6-2-5 となっています。私的には ムサシ・・・ 6-3-4 といったところが平均だと感じていますので、そこの線からいうとほぼ妥当な予想を出力しているんじゃないかと思います。
予想を振り返って知見を得る
まず全体的な総括から。
ページトップに挙げた2種類の予想、これはどちらも H2O の ディープラーニング による分類予測です。これらの予測方法の違いは以下です。
1、ブルー側は、単一の設定による分類予測です。使用した活性化関数は Rectifier
2、ピンク側はグリッドサーチによって活性化関数を枠ごとに設定しています。設定を変えたのはここだけです。
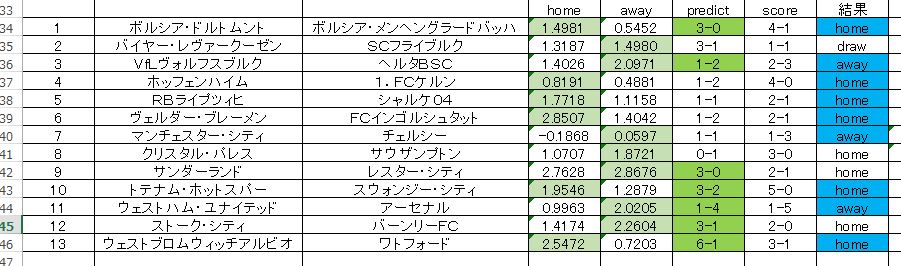
あらためて正解をマーキングした表を載せます。
少し濃いマーキングをした箇所が正解しているところです。単純な比較においてはピンク側の方が良い予測結果を残していますね。この結果からいうと、やはり対戦カードごとにチューニングをした方が良いのではないかと思えてきます。
H2O においては6種類の活性化関数が用意されています。グリッドサーチにおいてトップに示されるものが一番良くフィットするものとして提示されるわけですが、その評価関数は Log loss です。数値がゼロに近いほど良いと判断されます。
ただ僕の感触では、これを妄信するのはどうか? といった疑念もある。可能なら すべての活性化関数を試して、出力結果を検討するのもいいかと思います。手間はかかるけど得られるものもあるかもしれません。
さて、もうひとつの予測、今度はスコアの回帰分析について考えてみましょう。
予測手順は以下の通り。
先の分類予測で使用したデータをそのまま使います。アルゴリズムは同じくディープラーニングです。response_column をスコアの部分に指定するだけで回帰分析もできるようになります。ただスコア分類やゴール数の回帰に関しては活性化関数のグリッドサーチは行っておらず、初期設定のまま走らせています。理由は、単純に 忘れてしまったから です。まだ検証はしていませんが、仮にグリッドサーチを行って関数を選択していたら、違った結果が得られていたと思います。
では画像を確認します。
カラーマーキングの意味から説明します。
PREDICT は、スコアそのもを予測したものですが、その勝敗部分 だけに注目して正解にマーキングしました。全体的にはあんまり良い感じはしません。
濃いブルーは、回帰分析による数値の優劣だけに注目してマークしたものです。こちらは比較的 良い結果を残しています。単純にドローが少なかったのも要因ですが、スコアの回帰分析による優劣判断においては、ほぼ傾向を把握しているように感じます。完全ではないところが痛いけど。
まとめると、上の結果を見る限りでは、ゴール数の回帰分析による優劣判断が有効であると考えられます。また、分類予測においては、対戦カードごとにアルゴリズムのチューニングを個別に行うことも有効であると言えます。
分類予測も、ゴール数の回帰も、誤った予測をしている箇所がよく似ています。なんか興味深いですね。なぜなんだろ?




コメント